FIFO (先进先出) Netting一般指按时间顺序抵消正负值,直到一方耗尽。由于这个问题难度适中且可以用风格差异较大的多种方法解题,所以想和大家分享一下目前已经想到的解法。为了让大家更容易理解这个问题,示例如下:
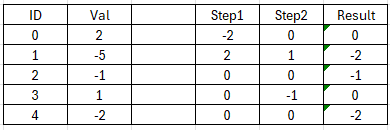
表格的Val字段的字段值分别为2,-5,-1,1,-2,要求2和-5抵消后,2变为0,-5变成-3,然后1和-3抵消后,1变为0,-3变成-2,最终Val字段的字段值更新为0, -2, -1, 0, -2。为了让初次接触的朋友更深入地了解这个问题,再提供一个例子:
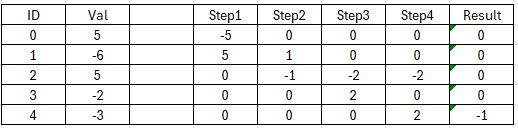
表格的Val字段的字段值分别为5,-6,5,-2,-3,步骤总结如下:
(1)5和-6抵消,5变为0,-6变为-1;
(2)-1和5抵消,-1变为0,5变成4;
(3)4和-2抵消,4变成2,-2变成0;
(4)2和-3抵消,2变成0,-3变成-1
最终Val字段的字段值更新为0, 0, 0, 0, -1。虽然这个问题给人一种无从入手的感觉,但结合生活的经验不难总结出以下流程(用例子一进行说明):
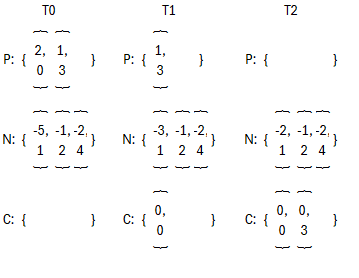
(1)把Val和ID的字段值分为两组,一组为P包括所有Val大于0的信息,另一组为N涵盖所有Val小于0的信息。
(2)完成第一次抵消后,2变成0以及-5变成为-3,把{0, 0}从P中移除放进C中
(3)完成第二次抵消后,1变成0以及-3变成为-2,把{0, 3}从P中移除放进C中
(4)留意到P已经空了,把N和C拼接起来,按ID大小升序排列。
直至P或者N变成为空集前,每一个步骤结束时P/N/C都会作为下一个步骤的自变量,所以需要使用递归解题,对应代码如下:
let
Source = Table.ToRows(DB),
P = List.Select(Source, each _{0} > 0),
N = List.Select(Source, each _{0} < 0),
Z = List.Select(Source, each _{0} = 0),
Processor = (p, n, c) =>
if
List.IsEmpty(p)
or
List.IsEmpty(n)
then
c ﹠ p ﹠ n
else
let
Top_P = p{0},
Tail_P = List.Skip(p, 1),
Top_N = n{0},
Tail_N = List.Skip(n, 1),
Sum = Top_P{0} + Top_N{0},
Outcome =
if
Sum < 0
then
@Processor(
Tail_P,
{{Sum, Top_N{1}}} ﹠ Tail_N,
{{0, Top_P{1}}} ﹠ c
)
else if
Sum > 0
then
@Processor(
{{Sum, Top_P{1}}} ﹠ Tail_P,
Tail_N,
{{0, Top_N{1}}} ﹠ c
)
else
@Processor(
Tail_P,
Tail_N,
{{0, Top_N{1}}, {0, Top_P{1}}} ﹠ c
)
in
Outcome,
Sorting =
List.Sort(
Processor(P, N, {}) ﹠ Z,
(x, y)=> Value.Compare(x{1}, y{1})
),
Result =
Table.FromRows(
Sorting,
type table [Val = number, ID = number]
)
in
Result
虽然以上解法简洁易懂,不过一旦行数达到5,000或以上时,就会出现超栈警告,说明人脑觉得很自然的思路对计算机来说未必高效。思考良久后,感觉以下方案(用例子一进行说明)应该会让电脑轻松不少:
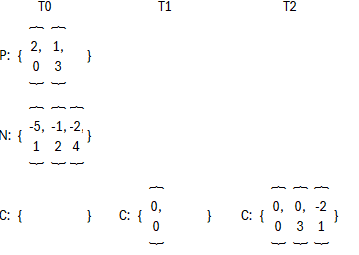
(1)第一步和上一种方案一样;
(2)完成第一次抵消后,2变成0以及-5变成为-3,把{0, 0}放进C;
(3)完成第二次抵消后,1变成0以及-3变成为-2,把{0, 3}以及{-2, 1}放进C;
(4)把ID为0或3对应的Val更新为0,把ID为1对应Val更新为-2
这个思路的关键在于要想办法在不修改P和N的前提下获得C,借鉴求累计和或移动平均的思路,不难得出以下解法:
let
Source = Table.ToRows(DB),
P =
List.Buffer(
List.Select(
Source,
each _{0} > 0
)
),
N =
List.Buffer(
List.Select(
Source,
each _{0} < 0
)
),
Cnt_P = List.Count(P),
Cnt_N = List.Count(N),
Common_Case =
List.Generate(
()=>
[
P_Idx = 0,
N_Idx = 0,
Net_Val = P{0}{0} + N{0}{0}
],
each [P_Idx] < Cnt_P and [N_Idx] < Cnt_N,
each
[
P_Idx = [P_Idx] + (if [Net_Val]<=0 then 1 else 0),
N_Idx = [N_Idx] + (if [Net_Val]>=0 then 1 else 0),
Net_Val =
let
New_P_Val = if P_Idx < Cnt_P then P{P_Idx}{0} else null,
New_N_Val = if N_Idx < Cnt_N then N{N_Idx}{0} else null,
New_Net_Val =
if
[Net_Val] = 0
then
New_P_Val + New_N_Val
else
[Net_Val] + (if [Net_Val] > 0 then New_N_Val else New_P_Val)
in
New_Net_Val
],
each
let
Cur_P = P{[P_Idx]},
Cur_N = N{[N_Idx]},
Is_P_End = ([P_Idx] <> Cnt_P - 1),
Is_N_End = ([N_Idx] <> Cnt_N - 1),
Is_End = Is_P_End and Is_N_End,
Outcome =
if
[Net_Val] > 0
then
if
Is_N_End
then
{{Cur_N, {0, Cur_N{1}}}}
else
{{Cur_N, {0, Cur_N{1}}}, {Cur_P, {[Net_Val], Cur_P{1}}}}
else if
[Net_Val] < 0
then
if
Is_P_End
then
{{Cur_P, {0, Cur_P{1}}}}
else
{{Cur_P, {0, Cur_P{1}}}, {Cur_N, {[Net_Val], Cur_N{1}}}}
else
{{Cur_N, {0, Cur_N{1}}}, {Cur_P, {0, Cur_P{1}}}}
in
Outcome
),
Sub =
List.ReplaceMatchingItems(
Source,
List.Combine(
List.Buffer(Common_Case)
)
),
To_Table =
Table.FromRows(
Sub,
type table [Val = number, ID =number]
),
Final_Result =
if
List.IsEmpty(P) or List.IsEmpty(N)
then
DB
else
To_Table
in
Final_Result
为配合List.ReplaceMatchingItems()对参数的要求,实际要计算的C比上图的要稍微复杂:{{{2,0},{0,0}},{{1,3},{0,3}},{{-5,1},{-2,1}}}。这个方案已经能处理百万级的数据了,通过观察这种量级的结果,不难发现还存在一种更高效的方案(用例子一进行说明):
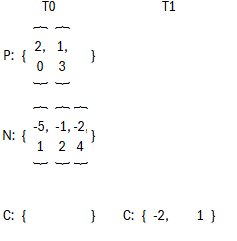
(1)第一步和前两种方案一样;
(2)找到N中最后一个会产生变化的Val以及其相对位置,构造出C: {-2, 1};
(3)如果源数据的Val大于0,全部更新为0;
(4)如果源数据的Val小于0且ID小于1,全部更新为0;
(5)如果源数据的Val小于0且ID大于1, Val保持不变,否则更新为-2
以上方案对应的代码:
let
P_TB =
Table.SelectRows(
DB,
each [Val] > 0
),
N_TB =
Table.SelectRows(
DB,
each [Val] < 0
),
P_Val =
List.Buffer(
Table.Column(
P_TB,
"Val"
)
),
P_ID =
List.Buffer(
Table.Column(
P_TB,
"ID"
)
),
P_Sum = List.Sum(P_Val),
N_Val =
List.Buffer(
Table.Column(
N_TB,
"Val"
)
),
N_ID =
List.Buffer(
Table.Column(
N_TB,
"ID"
)
),
N_Sum = List.Sum(N_Val),
Agg = P_Sum + N_Sum,
Info =
(pn_val as list, pn_id as list, s as number)=>
List.Generate(
()=> [PreVal = 0, n = -1],
each ([PreVal] + s) * s > 0,
each
[
PreVal = [PreVal] + pn_val{n},
n = [n] + 1
],
each
[
idx = pn_id{[n] + 1},
val = [PreVal] + pn_val{[n]+1} + s
]
),
Adj =
(pn_val as list, pn_id as list, s as number)=>
let
Final_Info = List.Last(Info(pn_val, pn_id, s)),
Idx = Record.Field(Final_Info, "idx"),
Net_Val = Record.Field(Final_Info, "val"),
Val_Adj =
Table.AddColumn(
DB,
"Val_Adj",
each if
[Val] * s >= 0
then
0
else if
[ID] < Idx
then
0
else if
[ID] > Idx
then
[Val]
else
Net_Val,
type number
),
Sub =
Table.RenameColumns(
Table.SelectColumns(
Val_Adj,
{"Val_Adj", "ID"}
),
{"Val_Adj", "Val"}
)
in
Sub,
Prelim =
if
Agg > 0
then
Adj(P_Val, P_ID, N_Sum)
else if
Agg < 0
then
Adj(N_Val, N_ID, P_Sum)
else
Table.TransformColumns(
DB,
{
"Val",
0,
type number
}
),
Output =
if
Table.IsEmpty(P_TB) or Table.IsEmpty(N_TB)
then
DB
else
Prelim
in
Output
如果P或N各占数据的一半,使用二分法处理百万级的数据大约只需进行Log2(500,000)≈19次循环就可以找到拐点,但由于List.Sum+List.Range比较慢,导致与从前往后找所需的用时接近,以下提供对应代码以供参考:
