如果匹配的对象不是离散数,区间的闭合方向不一致会使匹配稍微复杂一点,首先介绍一下演示用的参数表Para:
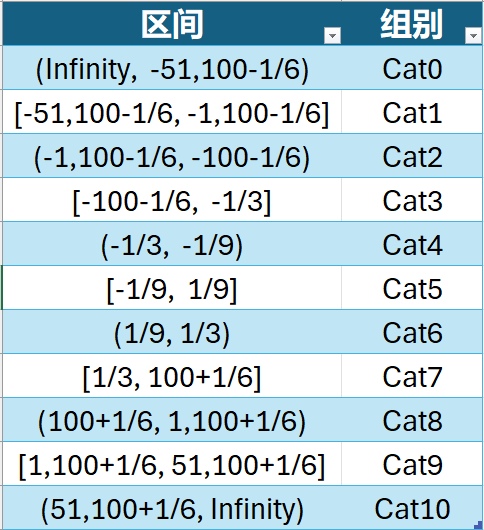
为了识别区间左右端的闭合性,需要两列布林型的字段:
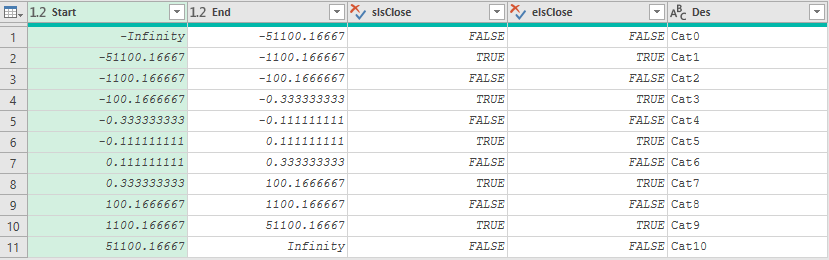
很显然由于需要枚举的数值数量无限多,枚举法是不适合非离散数的匹配,同时由于区间的闭合方向不一致,以List.PositionOf()为主体的方案也无法直接套用到这个问题中。不过,筛选参数表的方案稍稍调整一下就可以使用了,演示代码如下:
let
Buffering =
List.Buffer(
Table.ToRows(Para)
),
Add_TB =
Table.AddColumn(
DB,
"Des",
(x)=>
List.Select(
Buffering,
(y)=>
(
if
y{2} = true
then
y{0} <= x[Val]
else
y{0} < x[Val]
)
and
(
if
y{3} = true
then
y{1} >= x[Val]
else
y{1} > x[Val]
)
){0}{4},
type text
)
in
Add_TB
以上代码的大意为:
(1)通过List.Buffer()把列表化的参数表缓冲至内存;
(2)通过if把左右闭合的四种情况考虑进来,让List.Select选出唯一匹配的区间,最后深化出区间的描述
使用这种方法处理百万级的数据需时9.3秒左右。动态的多重if方案经过调整也可以用来解决这个问题,不过有个问题不是那么容易察觉到: 除非显式地在公式中指定Precision.Decimal,否则Power Query的number数据默认精度为Double, 比如:1/3会被显示为0.33333333333333331,并且大致上从0.33333333333333329到0.33333333333333334之间(包括两端)的数都被认为等于1/3。因此,需要确保参数表中的数值在转换为文字时需要保留足够的小数位,例如1/3应该被转换为"0.33333333333333331"而不是"0.33",演示代码如下:
let
Source =
Expression.Evaluate(
"(x)=>"
﹠
Text.Combine(
Table.TransformRows(
Table.RemoveLastN(Para, 1),
(x)=>
Text.Format(
"if x[Val] #{0} #{1} then #{2}",
{
if x[eIsClose] then "<=" else "<",
Number.ToText(x[End], "G17"),
Expression.Constant(x[Des])
}
)
)
﹠
{Expression.Constant(Table.Last(Para)[Des])},
" else "
)
)
in
Source
为了确保数字在被转换为文字后能保留足够的精度,需要选择G17作为Number.ToText()的第二个参数。以上函数作为Table.AddColumn()的第三个参数就可以获得匹配的结果,相同条件下处理百万级数据用时约6.6秒。最后介绍一下AI的思路: 以[0, 1/6]和(1/6, 1/3)这两个虚构区间为例,计算出1/6的下一个双精度浮点数x,把区间修改为[0, x)和[x, 1/3)就可以实现所有区间统一为左闭右开,但下一个浮点是很难计算的,AI构造的函数F如下:
(x as number) as number =>
let
abs = Number.Abs(x),
rsl =
if
abs < Min_Norm_EXP //Number.Power(2, -1022)
then
Number.Epsilon
else
Number.Power(
2,
Value.Subtract(
Number.RoundDown(
Number.Log(abs, 2),
0
),
52
)
)
in
rsl
然后需要更新参数表为Para_Adj:
let
s_adj =
Table.AddColumn(
Para,
"Start_Adj",
each if
[Start] = Number.NegativeInfinity
then
[Start]
else if
[sIsClose]
then
[Start]
else
[Start] + F([Start]),
type number
),
e_adj =
Table.AddColumn(
s_adj,
"End_Adj",
each if
[End] = Number.PositiveInfinity
then
[End]
else if
[eIsClose]
then
[End] + F([End])
else
[End],
type number
),
rsl = Table.SelectColumns(e_adj, {"Start_Adj", "End_Adj", "Des"})
in
rsl
这样所有区间都统一为左闭右开,筛选参数表法就可以简化为:
let
Buffering =
List.Buffer(
Table.ToRows(Para_Adj)
),
Add_TB =
Table.AddColumn(
DB,
"Des",
(x)=>
List.Select(
Buffering,
(y)=> y{0}<= x[Val] and y{1} > x[Val]
){0}{2},
type text
)
in
Add_TB
简化后运行时间稍微降低至8.7秒,由于区间闭合方向统一了,List.PositionOf()为主体的方案也能用了:
let
S =
List.Buffer(
Para_Adj[Start_Adj]
),
D =
List.Buffer(
Para_Adj[Des]
),
Add_TB =
Table.AddColumn(
DB,
"Des",
(x)=>
D{
List.PositionOf(
S,
x[Val],
Occurrence.Last,
(k, j)=> k <= j
)
},
type text
)
in
Add_TB
相同条件下以上代码的运行时间大约为8.3秒。由于统一闭合方向对于多重if的方案来说仅减少一个判断的步骤,可预见提升应该不显著。考虑性能和理解的难度,针对区间闭合不一致的问题,似乎应该首选多重if方案。